|

|
|

|
|
На каком языке программирования вам нужен симплекс-метод?
|
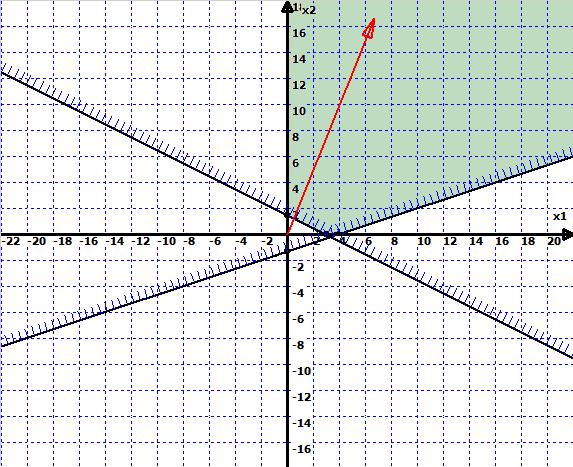
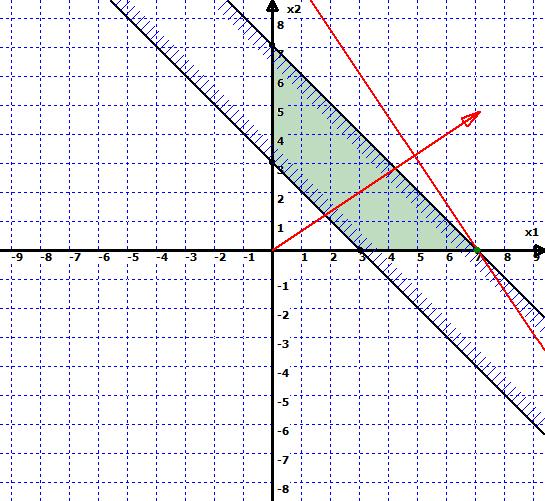
Решение задач линейного программирования графическим методом. Существуют два наиболее распространенных способа решения задач линейного программирования (ЗЛП): графический метод и симплекс-метод. Графический метод существенно нагляднее и обычно проще для понимания и решения (хотя занимает много времени, так как требует тщательного построения чертежа). Также этот метод позволяет практически одновременно найти решение на минимум и максимум, тогда как симплекс-методом придется делать 'два подхода'. Основные шаги по решению ЗПЛ графическим методом следующие: построить область допустимых решений задачи (выпуклый многоугольник), который определяется как пересечение полуплоскостей, соответствующих неравенствам задачи, построить линию уровня целевой функции, и, наконец, двигать линию уровня в нужном направлении, пока не достигнем крайней точки области - оптимальной точки (или множества). При этом можно найти единственное оптимальное решение (точку), множество (отрезок) или ни одного (область пустая или не ограниченная в нужном направлении). Решение задачи линейного программирования графическим методом включает следующие этапы: 1) На плоскости строят прямые ограничений. Определяют область образованную этими прямыми. Существует несколько вариантов: a). Область не ограничена. Т.е. ее ограничения не замкнуты, а направляющий вектор (вектор, составленный из коэффициентов целевой функциию) указывает в направлении бесконечности. В этом случае говорят, что задача имеет бесконечное множество решений. (Рис. 1)
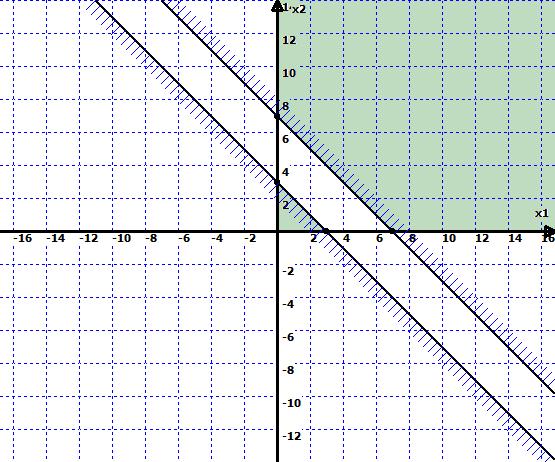
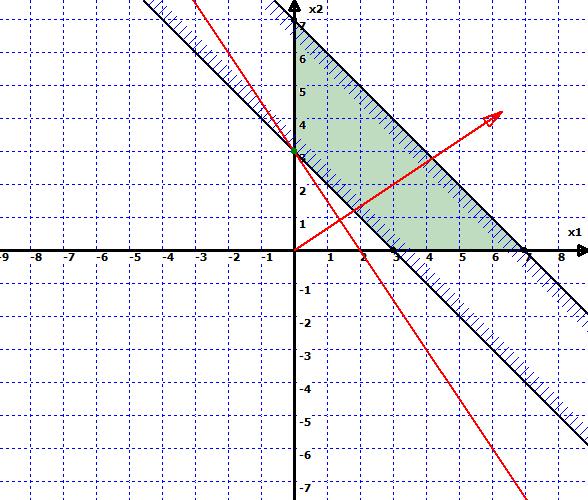
b). Область пуста. Т.е. ее ограничения несовместны. В этом случае говорят, что задача не имеет допустимого решения. (Рис. 2)
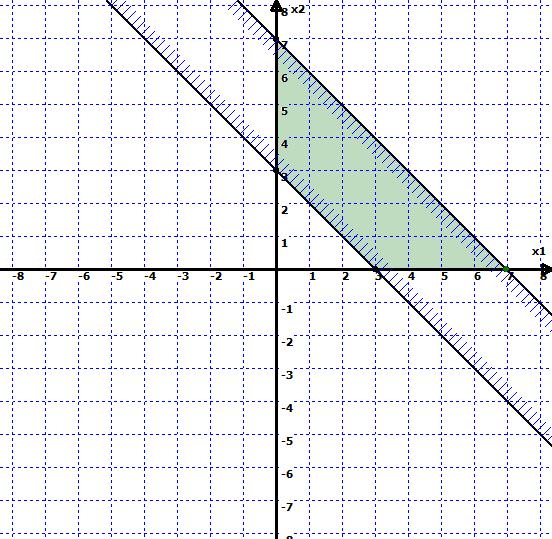
c). Область замкнута. В этом случае задача имеет единственное решения. (Рис. 3)
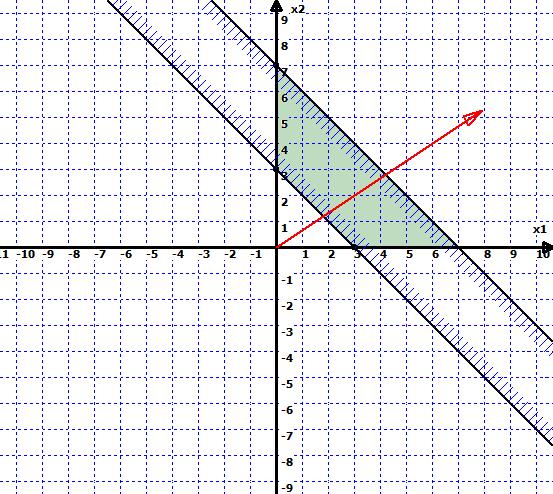
В одной из вершин получившейся плоскости (области), целевая функция достигает своего максимального или минимального значения, в зависимости от типа решаемой задачи. Можно просто перебрать все вершины, подставляя их в целевую функцию, и найти ее максимальное/минимальное значение, но это займет больше времени, особенно когда ограничений много. Поэтому, для нахождения решения, построим вектор, составленный из коэффициентов целевой функции. (Рис. 4).
Теперь построим прямую, параллельную данному вектору и будем параллельно двигать ее в направлении или против направления вектора, в зависимости от типа решаемой задачи. Если нас интересует максимальное решение, то двигаем прямую в направлении вектора до последнего касания обозначенной области. (Рис. 5).
Если задача на минимальное решение, то параллельно двигаем прямую в противоположенном направлении от вектора, до последнего касания обозначенной области. (Рис. 6).
|
| Договор оферты |
|
Copyright © MathZone.Ru, 2012 - 2024 email: alex_ey@mail.ru |